聚苯乙烯顆粒的稀相氣力輸送系統
發布時間:2018-08-07 15:20 ?|?作者: 氣力輸送 ?|?來源: 未知
聚苯乙烯顆粒的稀相氣力輸送系統:管道橫截面上的壓降曲線和顆粒分布
在塑料粒料的氣力輸送過程中,已經觀察到具有相似物理特性的材料可能在壓降方面產生顯著差異。 在這項工作中,從實驗角度展示了具有圓形橫截面的載有顆粒的2.7米長水平通道中的壓降。 對圓柱形聚苯乙烯珠粒進行實驗,平均直徑為3.2mm,質量載荷為0.06-0.11(kg顆粒/ kg氣體)。 研究了空氣質量流量在0.085kg / s至0.170kg / s的范圍內。 壓降曲線顯示為空氣速度和顆粒載荷的函數。 響應面法對空氣速度,粒子載荷及其交叉關系表現出高度統計學意義。
關鍵詞:氣力輸送系統; 顆粒狀固體; 聚苯乙烯; 粒子分布; 壓力損失。
輸送管道中的固體流動通常通過應用兩種不同的流動技術進行:密相和稀相。 在致密相中,施加高濃度的固體,通常大于30%v / v,速度為1-5m / s。 密相狀態具有高的采集,操作和維護成本,因為它需要高氣壓(壓力高于20 mbar / m)。 稀相輸送在低于1%v / v的固體濃度和高于20m / s的速度下運行。 稀相方案成本較低,但在低運輸速度下會引起不規則的管道磨損,主要是在水平管道的下部。
在稀相中氣動輸送系統的性能受壓降的影響很大,而壓降又取決于幾個參數,例如材料特性,管道設計和氣流。
本研究的目的是獲得圓柱形聚苯乙烯顆粒的壓降曲線,并分析空氣速度和固體載荷對壓降的影響。 響應面法用于分析空氣速度和固體載荷對壓降響應的影響。
實驗裝置的圓柱形通道的總長度為4.2米。 通道的第一部分長1.5米,用于在聚合物顆粒的進料點之前獲得完全發展的氣流。 圓柱形通道的初始部分具有流量調節器,其位于鼓風機后0.9m處,其用于使管流中的速度分布均勻化。 流量調節器還旨在加速形成完全發展的湍流速度分布,其在調節器下游約25個直徑處獲得(Xiong等人,2005)。
實驗裝置的主要部件由圓柱形通道組成,放置在顆粒的進料點之后,長2.7米,內徑117毫米。 這種配置允許建立二維流動條件,其中由于顆粒沉降,重力破壞了兩相流中的圓柱對稱( 圖1和2 )。
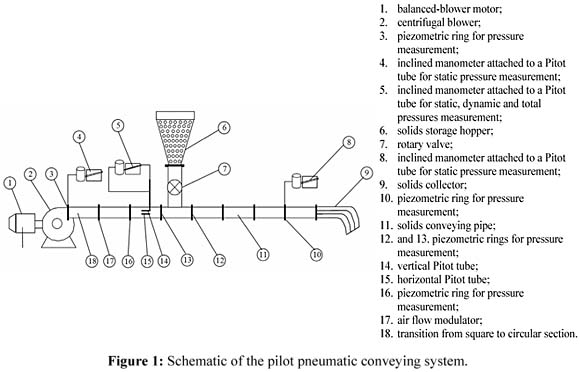

通過離心式鼓風機(引持環保)引入空氣,其具有100mm直徑的半開式葉片,203mm直徑的吸入管線和102mm方形排出部分,其連接至1Hp可變旋轉馬達,其中兩個額外的軸承是增加(平衡鼓風機馬達)來評估機械功率。
通過皮托管測量總壓力和靜壓。 這些管由兩根190mm長的“L”形同軸管組成。 內管的內徑為3毫米,外管的內徑為8毫米,按照ASME規范制造。 總壓力通過皮托管的中心管獲得,而靜壓通過放置在皮托管外管壁中的小孔獲得。 動態壓力確定為總壓力和靜壓力之間的差值。 皮托管放置在第一個測壓環后0.13米處和流量調節器后0.53米處。
在流動調節器之后,分別將第一,第二,第三和第四測壓環放置在0.40米,0.60米,1.20米和3.00米處。
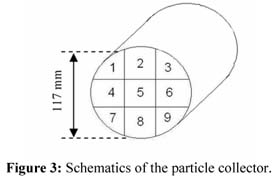
借助于帶有六個徑向葉片的旋轉閥將固體從進料容器送入輸送管,測量為92mm×42mm,直徑為76.2mm。 將固體排放到位于水平氣動輸送機末端的收集器模塊中。 顆粒分布分析模塊由九個方形截面的鋁管組成,尼龍袋連接在其上以收集固體顆粒( 圖3 )。 負載 μ (固體質量流量/空氣質量流量)由氣流閥和旋轉閥的相互作用控制。
在測試中使用聚苯乙烯顆粒(PS)并由BASF提供。 聚苯乙烯顆粒的性質列于表1中 。

通過將固體質量流速設定為0.085kg / s,0.13kg / s和0.17kg / s(此處分別稱為G 1 ,G 2和G 3 )來建立作為空氣速度的函數的聚苯乙烯壓降特性曲線。 。 速度從5到35米/秒變化,載體上的壓力用連接到傾斜壓力計的測壓環測量。 在這些條件下的最小和最大顆粒負載量分別為0.5kg顆粒/ kg空氣和7.8kg顆粒/ kg空氣。
聚苯乙烯在管道中的分布是根據安裝在輸送管末端的九管收集模塊中的固體質量確定的; 管道編號如圖3所示。 在每個袋中收集的質量用于計算每單位面積的質量分數,然后允許計算聚苯乙烯在管的橫截面中對于所有空氣速度和固體質量流速的分散。
計算九個收集器的顆粒密度,并且還使用表面響應方法處理這些點。 使用軟件Statistica v7.0基于使用距離加權最小二乘法的數據內插來生成粒子分布輪廓。 應用該方法是因為它為非對稱輪廓提供了更好的數據擬合。
將水平和垂直方向上的壓降測量值歸一化為 ΔP/ L,其中L是壓力抽頭之間的距離。 圖4顯示了聚苯乙烯顆粒在水平方向上的壓降與載荷和空氣速度的關系。 圖4中的A'B'部分表示由整個水平傳輸線中的空氣流(無固體流速G 0 = 0)引起的壓降。 由于內部摩擦,空氣對壁摩擦和流動擾動,壓力隨著速度的增加而增加。
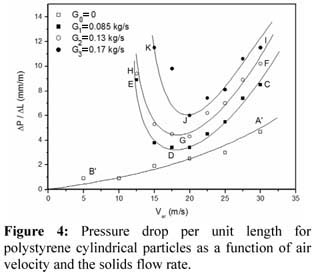
圖4中的CDE部分表示固體流速為0.085kg / s(G 1 )時的壓降曲線。 高風速(25米/秒)導致相對較高的壓降。 隨著空氣速度降低并且固體質量流速保持恒定,壓降達到最小點,然后由于水平管下部的固體沉降而增加。 對于所有固體流速(G 2 = 0.13kg / s和G 3 = 0.17kg / s)觀察到相同的行為。
響應面法用于分析操作條件對聚苯乙烯顆粒壓降的影響。 表2列出了壓降的因素擾動分析。 結果顯示,在99%的置信水平下,固體載荷和空氣速度的二次效應(v 2 )具有統計學意義(p <0.01)。 兩種操作條件對壓降都有積極影響,這意味著固體載荷或空氣速度的增加傾向于增加聚苯乙烯珠粒的壓降。 在恒定空氣速度下,總壓力梯度隨著固體質量流速的增加而增加。 高固體流速下的壓降增加可歸因于管道中較高的橫截面固體濃度,從而對通過系統的空氣流動產生額外的阻力。
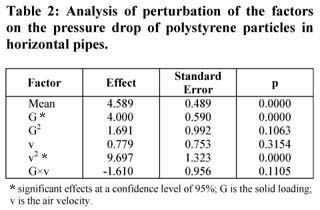
空氣速度二次項的99%置信水平的正面意義表明,空氣速度的增加對壓降的影響遠大于固體載荷。 空氣速度和固體載荷之間的交叉相互作用是負的,這意味著在某些操作條件下,可以找到壓降的最小值, 如圖4所示 。
管道中氣流的壓降(G = 0)可用公式(1)表示:
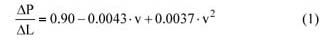
水平管道中兩相流的壓降(G = 0.085至G = 0.17)可用公式(2)(單位為mm / m)或公式(3)(單位為Pa / m)表示:
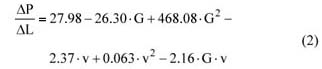
水平管道中兩相流的壓降(G = 0.085至G = 0.17)可用公式(2)(單位為mm / m)或公式(3)(單位為Pa / m)表示:
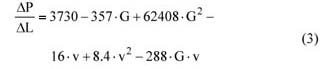
其中 ΔP/ ΔL是壓降(Pa / m),G是固體流速(kg / s),v是空氣流速(m / s)。
為了對任何管道直徑普遍有效,可以重新定義等式(3),如公式(4)所示:
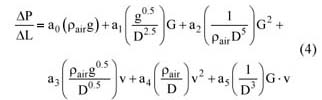
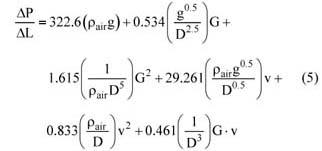
其中 ΔP/ ΔL是壓降(Pa / m),D是管道直徑(m),G是固體流速(kg / s),g是重力加速度(m / s 2 ) v是空氣流量(m / s), ρa 是空氣密度(kg / m 3 )。
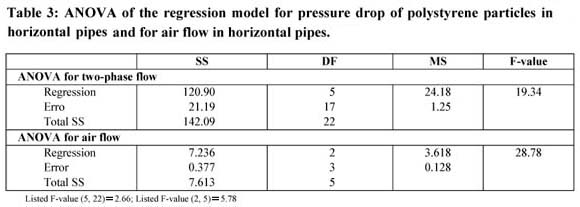
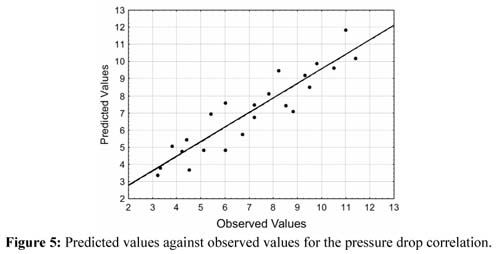
通過F檢驗驗證了水平管中聚苯乙烯顆粒壓降和水平管中氣流壓降的回歸模型( 表3 )。 F檢驗的結果顯示,計算的F值比列出的F值高出4倍以上(95%置信水平),表明回歸模型是有效的,可用于預測水平管道中聚苯乙烯顆粒的壓降。 預測值和觀測值的圖示于圖5中 。
當空氣流速很高時,固體完全懸浮在空氣流中。 隨著空氣速度的降低,固體移動得更慢,并傾向于沉降在管道的下部。 當空氣速度不足以保持所有顆粒懸浮時,顆粒開始在管道底部沉降,直到橫截面完全堵塞(Rhodes,2000)。 此時,固體沿管道底部以密相輸送。 這一點標志著氣動輸送的稀相和密相之間在水平線上的邊界。
Vásquez等。 (2008)研究了4mm聚乙烯顆粒(硬顆粒和軟顆粒)的壓降曲線,速度在15和30m / s之間,固體載荷/空氣質量在0.5和2.5之間。 Vásquez等人獲得的結果。 (2008)類似于本文獲得的聚苯乙烯顆粒的壓降。 Vásquez等。 (2008)聲稱增加的壓降部分是由于顆粒在通過輸送系統的過程中必須多次重新加速。 另外,強烈的彈跳增加了固體和空氣之間的軸向速度差異,增加了顆粒上的阻力。
Tomita和Asou(2009)研究了聚乙烯顆粒在水平管道中以非常低的速度(<8 m / s)輸送。 他們觀察到高壓力損失,就像本研究報告的低氣流速度一樣,也可以通過類似于公式(3)的方程擬合。 Pahk和Klinzing(2008)對聚苯乙烯顆粒觀察到相同的典型結果,但是在高空氣速度和稍大的顆粒直徑(3.9mm)下觀察到。
水平管道中氣動輸送的壓降也可以通過考慮氣流速度,管道直徑,氣體密度,顆粒負載和顆粒摩擦系數的公式來擬合。 然而,顆粒摩擦系數難以計算,并且其估計存在若干相關性。 通常,顆粒摩擦系數取決于氣流速度,顆粒速度,管道直徑,氣體密度,顆粒負荷,阻力系數,顆粒直徑和氣體粘度(Klinzing等,1997)。 這里提出的用于估算聚苯乙烯顆粒的水平氣力輸送中的壓降的等式可以用作更復雜的等式的替代。
圖6顯示,即使遠離最小壓降點,也可能在管的橫截面中出現不均勻的顆粒分布。 在最高風速(23 m / s)和最低固體流速(0.085 kg / s)下,固體大部分在管道底部附近運輸,83%的聚苯乙烯顆粒存在于收集器中7 ,8和9( 圖3 )。 在任何操作條件下,聚苯乙烯顆粒在管道中的輸送不均勻分布。 當氣動輸送在高風速和低聚乙烯流速下運行時,發現了最佳分布。 即便如此,68%的顆粒沿管道底部移動,只有16%的顆粒被收集在管道的上層。
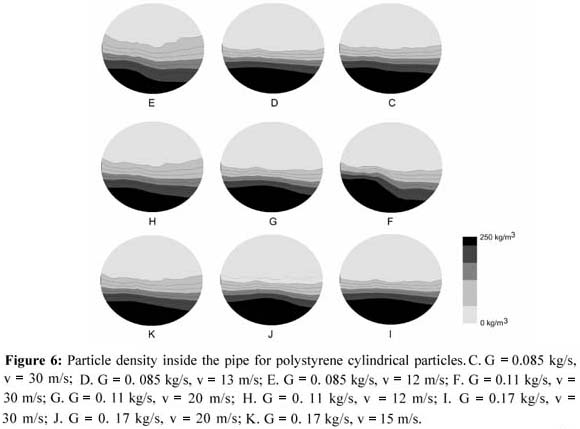
在該工作中獲得的管的橫截面中的顆粒分布類似于通過諸如擴展激光多普勒測速儀(LDA)的先進技術獲得的水平管流的顆粒密度分布。 Lu等人。 (2009)通過使用擴展的LDA技術研究了玻璃珠的運輸,并報道了類似于本文獲得的顆粒分布。
這里應用的所有條件的斯托克斯數高于1,表明顆粒運動與載氣流無關,因為它無法響應其變化。 對于兩相流計算的最低斯托克斯數是1.53,在5m / s的空氣流速下獲得,其接近于顆粒的快速和慢響應時間與空氣速度變化之間的理論邊界。 對于兩相流計算的最高斯托克斯數是10.7,在空氣流速為35m / s時獲得。
結果表明,作為空氣速度和固體質量流量函數的壓降曲線必須與管道橫截面中顆粒分布的數據相結合,以加強稀相氣動的設計和分析。輸送系統。
聚苯乙烯在管道中的水平氣動輸送中呈現不均勻的顆粒分布。 圓柱形聚苯乙烯顆粒的輸送主要在管的下部,即使在低固體載荷和高空氣速度下也是如此。 當系統在高風速和低聚苯乙烯負載下運行時,發現了最佳分布。 結果表明研究顆粒分散和系統特征曲線的重要性
參考
Adam,O.,UntersuchungenüberdieVorgängeinfestoffbeladenenGasströmungen。 Forschungsberichte des Landes Nordrhein-Westfalen。 Westdeutscher Verlag,Köln(1960)。 [ 鏈接 ]
Hirota,M.,Sogo,Y.,Marutani,T。和Suzuki,M。,粉末的機械性能對斜管氣力輸送的影響。 Powder Tech。,122,150(2002)。 [ 鏈接 ]
Klinzing,GE,Marcus,RD,Rizk,F。和Leung,LS,固體氣力輸送:理論和實踐方法。 Chapman&Hall,倫敦(1997年)。 [ 鏈接 ]
Kuang,SB,Chu,KW,Yu,AB,Zou,ZS和Feng,YQ,氣力輸送中水平段塞流的計算研究。 Ind.Eng。 化學。 Res。,47,470(2008)。 [ 鏈接 ]
Lain,S.,Sommerfeld,M。和Quintero,B。水平圓管中固體顆粒氣力輸送中二次流動的數值模擬。 布拉茲。 J. Chem。 Eng。,26,583(2009)。 [ 鏈接 ]
Li,H。和Tomita,Y。水平稀釋旋流氣力輸送中的顆粒速度和濃度特性。 Powder Tech。,107,144(2000)。 [ 鏈接 ]
Lu,Y.,Glass,DH和Easson,WJ,通過擴展LDA技術研究氣固水平管道流動中的顆粒行為。 Fuel,88,2520(2009)。 [ 鏈接 ]
Marcus,RD,Leung,LS和Klinzing,GE,固體氣力輸送:理論和實踐方法。 查普曼和霍爾,紐約(1990年)。 [ 鏈接 ]
Molerus,O.,概??述:固體的氣動輸送。 Powder Tech。,88,309(1996)。 [ 鏈接 ]
Pahk,JB和Klinzing,GE,兩種不同塑料顆粒的稀相氣力輸送的流動特性比較。 J. Chin。 研究所。 化學。 Eng。,39,148(2008)。 [ 鏈接 ]
Rhodes,M。,粒子技術簡介。 John Wiley&Sons,紐約(2000年)。 [ 鏈接 ]
Sommerfeld,M。水平通道中湍流氣體 - 粒子流碰撞效應的分析:第一部分。粒子輸運。 詮釋。 J. Multiph。 Flow,29,675(2003)。 [ 鏈接 ]
Sommerfeld,M。和Lain,S。從基本過程到工業粒子流量的數值預測。 Multiph。 科學。 Tech。,21,123(2009)。 [ 鏈接 ]
Tomita,Y。和Asou,H。,在水平管道中低速氣動輸送粗顆粒。 Powder Tech。,196,14(2009)。 [ 鏈接 ]
Tsuji,Y。和Morikawa,Y。LDV測量水平管道中的空氣 - 固體兩相流。 J. Fluid Mech。,120,385(1982)。 [ 鏈接 ]
Tsuji,Y。和Morikawa,Y。LDV測量垂直管道中的空氣 - 固體兩相流。 J. Fluid Mech。,139,417(1984)。 [ 鏈接 ]
Vásquez,N.,Jacob,K.,Cocco,R.,Dhodapkar,S。和Klinzing,GE,粒子彈跳的可視化分析及其對稀相氣力輸送中壓降的影響。 Powder Tech。,179,170(2008)。 [ 鏈接 ]
Xiong,W.,Kalkühler,K。和Merzhirch,W。,流量調節器下游的速度和湍流的測量。 In:流體計量流體力學(Ed.Merzkirch,W。),Springer,Berlin,pp.61-78(2005)。 [ 鏈接 ]
在塑料粒料的氣力輸送過程中,已經觀察到具有相似物理特性的材料可能在壓降方面產生顯著差異。 在這項工作中,從實驗角度展示了具有圓形橫截面的載有顆粒的2.7米長水平通道中的壓降。 對圓柱形聚苯乙烯珠粒進行實驗,平均直徑為3.2mm,質量載荷為0.06-0.11(kg顆粒/ kg氣體)。 研究了空氣質量流量在0.085kg / s至0.170kg / s的范圍內。 壓降曲線顯示為空氣速度和顆粒載荷的函數。 響應面法對空氣速度,粒子載荷及其交叉關系表現出高度統計學意義。
關鍵詞:氣力輸送系統; 顆粒狀固體; 聚苯乙烯; 粒子分布; 壓力損失。
輸送管道中的固體流動通常通過應用兩種不同的流動技術進行:密相和稀相。 在致密相中,施加高濃度的固體,通常大于30%v / v,速度為1-5m / s。 密相狀態具有高的采集,操作和維護成本,因為它需要高氣壓(壓力高于20 mbar / m)。 稀相輸送在低于1%v / v的固體濃度和高于20m / s的速度下運行。 稀相方案成本較低,但在低運輸速度下會引起不規則的管道磨損,主要是在水平管道的下部。
在稀相中氣動輸送系統的性能受壓降的影響很大,而壓降又取決于幾個參數,例如材料特性,管道設計和氣流。
本研究的目的是獲得圓柱形聚苯乙烯顆粒的壓降曲線,并分析空氣速度和固體載荷對壓降的影響。 響應面法用于分析空氣速度和固體載荷對壓降響應的影響。
材料和方法
實驗裝置
實驗裝置的圓柱形通道的總長度為4.2米。 通道的第一部分長1.5米,用于在聚合物顆粒的進料點之前獲得完全發展的氣流。 圓柱形通道的初始部分具有流量調節器,其位于鼓風機后0.9m處,其用于使管流中的速度分布均勻化。 流量調節器還旨在加速形成完全發展的湍流速度分布,其在調節器下游約25個直徑處獲得(Xiong等人,2005)。
實驗裝置的主要部件由圓柱形通道組成,放置在顆粒的進料點之后,長2.7米,內徑117毫米。 這種配置允許建立二維流動條件,其中由于顆粒沉降,重力破壞了兩相流中的圓柱對稱( 圖1和2 )。


通過離心式鼓風機(引持環保)引入空氣,其具有100mm直徑的半開式葉片,203mm直徑的吸入管線和102mm方形排出部分,其連接至1Hp可變旋轉馬達,其中兩個額外的軸承是增加(平衡鼓風機馬達)來評估機械功率。
通過皮托管測量總壓力和靜壓。 這些管由兩根190mm長的“L”形同軸管組成。 內管的內徑為3毫米,外管的內徑為8毫米,按照ASME規范制造。 總壓力通過皮托管的中心管獲得,而靜壓通過放置在皮托管外管壁中的小孔獲得。 動態壓力確定為總壓力和靜壓力之間的差值。 皮托管放置在第一個測壓環后0.13米處和流量調節器后0.53米處。
在流動調節器之后,分別將第一,第二,第三和第四測壓環放置在0.40米,0.60米,1.20米和3.00米處。
借助于帶有六個徑向葉片的旋轉閥將固體從進料容器送入輸送管,測量為92mm×42mm,直徑為76.2mm。 將固體排放到位于水平氣動輸送機末端的收集器模塊中。 顆粒分布分析模塊由九個方形截面的鋁管組成,尼龍袋連接在其上以收集固體顆粒( 圖3 )。 負載 μ (固體質量流量/空氣質量流量)由氣流閥和旋轉閥的相互作用控制。

材料
在測試中使用聚苯乙烯顆粒(PS)并由BASF提供。 聚苯乙烯顆粒的性質列于表1中 。

實驗
通過將固體質量流速設定為0.085kg / s,0.13kg / s和0.17kg / s(此處分別稱為G 1 ,G 2和G 3 )來建立作為空氣速度的函數的聚苯乙烯壓降特性曲線。 。 速度從5到35米/秒變化,載體上的壓力用連接到傾斜壓力計的測壓環測量。 在這些條件下的最小和最大顆粒負載量分別為0.5kg顆粒/ kg空氣和7.8kg顆粒/ kg空氣。
聚苯乙烯在管道中的分布是根據安裝在輸送管末端的九管收集模塊中的固體質量確定的; 管道編號如圖3所示。 在每個袋中收集的質量用于計算每單位面積的質量分數,然后允許計算聚苯乙烯在管的橫截面中對于所有空氣速度和固體質量流速的分散。
計算九個收集器的顆粒密度,并且還使用表面響應方法處理這些點。 使用軟件Statistica v7.0基于使用距離加權最小二乘法的數據內插來生成粒子分布輪廓。 應用該方法是因為它為非對稱輪廓提供了更好的數據擬合。
結果與討論
將水平和垂直方向上的壓降測量值歸一化為 ΔP/ L,其中L是壓力抽頭之間的距離。 圖4顯示了聚苯乙烯顆粒在水平方向上的壓降與載荷和空氣速度的關系。 圖4中的A'B'部分表示由整個水平傳輸線中的空氣流(無固體流速G 0 = 0)引起的壓降。 由于內部摩擦,空氣對壁摩擦和流動擾動,壓力隨著速度的增加而增加。

圖4中的CDE部分表示固體流速為0.085kg / s(G 1 )時的壓降曲線。 高風速(25米/秒)導致相對較高的壓降。 隨著空氣速度降低并且固體質量流速保持恒定,壓降達到最小點,然后由于水平管下部的固體沉降而增加。 對于所有固體流速(G 2 = 0.13kg / s和G 3 = 0.17kg / s)觀察到相同的行為。
響應面法用于分析操作條件對聚苯乙烯顆粒壓降的影響。 表2列出了壓降的因素擾動分析。 結果顯示,在99%的置信水平下,固體載荷和空氣速度的二次效應(v 2 )具有統計學意義(p <0.01)。 兩種操作條件對壓降都有積極影響,這意味著固體載荷或空氣速度的增加傾向于增加聚苯乙烯珠粒的壓降。 在恒定空氣速度下,總壓力梯度隨著固體質量流速的增加而增加。 高固體流速下的壓降增加可歸因于管道中較高的橫截面固體濃度,從而對通過系統的空氣流動產生額外的阻力。

空氣速度二次項的99%置信水平的正面意義表明,空氣速度的增加對壓降的影響遠大于固體載荷。 空氣速度和固體載荷之間的交叉相互作用是負的,這意味著在某些操作條件下,可以找到壓降的最小值, 如圖4所示 。
管道中氣流的壓降(G = 0)可用公式(1)表示:
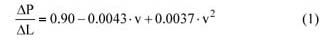
水平管道中兩相流的壓降(G = 0.085至G = 0.17)可用公式(2)(單位為mm / m)或公式(3)(單位為Pa / m)表示:
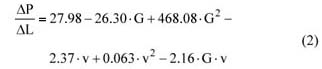
水平管道中兩相流的壓降(G = 0.085至G = 0.17)可用公式(2)(單位為mm / m)或公式(3)(單位為Pa / m)表示:
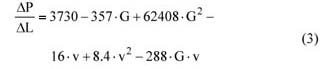
其中 ΔP/ ΔL是壓降(Pa / m),G是固體流速(kg / s),v是空氣流速(m / s)。
為了對任何管道直徑普遍有效,可以重新定義等式(3),如公式(4)所示:
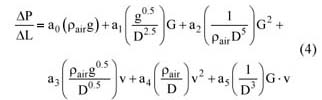
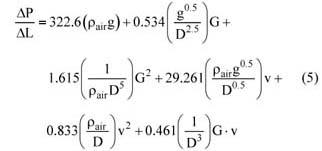
其中 ΔP/ ΔL是壓降(Pa / m),D是管道直徑(m),G是固體流速(kg / s),g是重力加速度(m / s 2 ) v是空氣流量(m / s), ρa 是空氣密度(kg / m 3 )。
通過F檢驗驗證了水平管中聚苯乙烯顆粒壓降和水平管中氣流壓降的回歸模型( 表3 )。 F檢驗的結果顯示,計算的F值比列出的F值高出4倍以上(95%置信水平),表明回歸模型是有效的,可用于預測水平管道中聚苯乙烯顆粒的壓降。 預測值和觀測值的圖示于圖5中 。


當空氣流速很高時,固體完全懸浮在空氣流中。 隨著空氣速度的降低,固體移動得更慢,并傾向于沉降在管道的下部。 當空氣速度不足以保持所有顆粒懸浮時,顆粒開始在管道底部沉降,直到橫截面完全堵塞(Rhodes,2000)。 此時,固體沿管道底部以密相輸送。 這一點標志著氣動輸送的稀相和密相之間在水平線上的邊界。
Vásquez等。 (2008)研究了4mm聚乙烯顆粒(硬顆粒和軟顆粒)的壓降曲線,速度在15和30m / s之間,固體載荷/空氣質量在0.5和2.5之間。 Vásquez等人獲得的結果。 (2008)類似于本文獲得的聚苯乙烯顆粒的壓降。 Vásquez等。 (2008)聲稱增加的壓降部分是由于顆粒在通過輸送系統的過程中必須多次重新加速。 另外,強烈的彈跳增加了固體和空氣之間的軸向速度差異,增加了顆粒上的阻力。
Tomita和Asou(2009)研究了聚乙烯顆粒在水平管道中以非常低的速度(<8 m / s)輸送。 他們觀察到高壓力損失,就像本研究報告的低氣流速度一樣,也可以通過類似于公式(3)的方程擬合。 Pahk和Klinzing(2008)對聚苯乙烯顆粒觀察到相同的典型結果,但是在高空氣速度和稍大的顆粒直徑(3.9mm)下觀察到。
水平管道中氣動輸送的壓降也可以通過考慮氣流速度,管道直徑,氣體密度,顆粒負載和顆粒摩擦系數的公式來擬合。 然而,顆粒摩擦系數難以計算,并且其估計存在若干相關性。 通常,顆粒摩擦系數取決于氣流速度,顆粒速度,管道直徑,氣體密度,顆粒負荷,阻力系數,顆粒直徑和氣體粘度(Klinzing等,1997)。 這里提出的用于估算聚苯乙烯顆粒的水平氣力輸送中的壓降的等式可以用作更復雜的等式的替代。
圖6顯示,即使遠離最小壓降點,也可能在管的橫截面中出現不均勻的顆粒分布。 在最高風速(23 m / s)和最低固體流速(0.085 kg / s)下,固體大部分在管道底部附近運輸,83%的聚苯乙烯顆粒存在于收集器中7 ,8和9( 圖3 )。 在任何操作條件下,聚苯乙烯顆粒在管道中的輸送不均勻分布。 當氣動輸送在高風速和低聚乙烯流速下運行時,發現了最佳分布。 即便如此,68%的顆粒沿管道底部移動,只有16%的顆粒被收集在管道的上層。

在該工作中獲得的管的橫截面中的顆粒分布類似于通過諸如擴展激光多普勒測速儀(LDA)的先進技術獲得的水平管流的顆粒密度分布。 Lu等人。 (2009)通過使用擴展的LDA技術研究了玻璃珠的運輸,并報道了類似于本文獲得的顆粒分布。
這里應用的所有條件的斯托克斯數高于1,表明顆粒運動與載氣流無關,因為它無法響應其變化。 對于兩相流計算的最低斯托克斯數是1.53,在5m / s的空氣流速下獲得,其接近于顆粒的快速和慢響應時間與空氣速度變化之間的理論邊界。 對于兩相流計算的最高斯托克斯數是10.7,在空氣流速為35m / s時獲得。
結果表明,作為空氣速度和固體質量流量函數的壓降曲線必須與管道橫截面中顆粒分布的數據相結合,以加強稀相氣動的設計和分析。輸送系統。
結論
聚苯乙烯在管道中的水平氣動輸送中呈現不均勻的顆粒分布。 圓柱形聚苯乙烯顆粒的輸送主要在管的下部,即使在低固體載荷和高空氣速度下也是如此。 當系統在高風速和低聚苯乙烯負載下運行時,發現了最佳分布。 結果表明研究顆粒分散和系統特征曲線的重要性
參考
Adam,O.,UntersuchungenüberdieVorgängeinfestoffbeladenenGasströmungen。 Forschungsberichte des Landes Nordrhein-Westfalen。 Westdeutscher Verlag,Köln(1960)。 [ 鏈接 ]
Hirota,M.,Sogo,Y.,Marutani,T。和Suzuki,M。,粉末的機械性能對斜管氣力輸送的影響。 Powder Tech。,122,150(2002)。 [ 鏈接 ]
Klinzing,GE,Marcus,RD,Rizk,F。和Leung,LS,固體氣力輸送:理論和實踐方法。 Chapman&Hall,倫敦(1997年)。 [ 鏈接 ]
Kuang,SB,Chu,KW,Yu,AB,Zou,ZS和Feng,YQ,氣力輸送中水平段塞流的計算研究。 Ind.Eng。 化學。 Res。,47,470(2008)。 [ 鏈接 ]
Lain,S.,Sommerfeld,M。和Quintero,B。水平圓管中固體顆粒氣力輸送中二次流動的數值模擬。 布拉茲。 J. Chem。 Eng。,26,583(2009)。 [ 鏈接 ]
Li,H。和Tomita,Y。水平稀釋旋流氣力輸送中的顆粒速度和濃度特性。 Powder Tech。,107,144(2000)。 [ 鏈接 ]
Lu,Y.,Glass,DH和Easson,WJ,通過擴展LDA技術研究氣固水平管道流動中的顆粒行為。 Fuel,88,2520(2009)。 [ 鏈接 ]
Marcus,RD,Leung,LS和Klinzing,GE,固體氣力輸送:理論和實踐方法。 查普曼和霍爾,紐約(1990年)。 [ 鏈接 ]
Molerus,O.,概??述:固體的氣動輸送。 Powder Tech。,88,309(1996)。 [ 鏈接 ]
Pahk,JB和Klinzing,GE,兩種不同塑料顆粒的稀相氣力輸送的流動特性比較。 J. Chin。 研究所。 化學。 Eng。,39,148(2008)。 [ 鏈接 ]
Rhodes,M。,粒子技術簡介。 John Wiley&Sons,紐約(2000年)。 [ 鏈接 ]
Sommerfeld,M。水平通道中湍流氣體 - 粒子流碰撞效應的分析:第一部分。粒子輸運。 詮釋。 J. Multiph。 Flow,29,675(2003)。 [ 鏈接 ]
Sommerfeld,M。和Lain,S。從基本過程到工業粒子流量的數值預測。 Multiph。 科學。 Tech。,21,123(2009)。 [ 鏈接 ]
Tomita,Y。和Asou,H。,在水平管道中低速氣動輸送粗顆粒。 Powder Tech。,196,14(2009)。 [ 鏈接 ]
Tsuji,Y。和Morikawa,Y。LDV測量水平管道中的空氣 - 固體兩相流。 J. Fluid Mech。,120,385(1982)。 [ 鏈接 ]
Tsuji,Y。和Morikawa,Y。LDV測量垂直管道中的空氣 - 固體兩相流。 J. Fluid Mech。,139,417(1984)。 [ 鏈接 ]
Vásquez,N.,Jacob,K.,Cocco,R.,Dhodapkar,S。和Klinzing,GE,粒子彈跳的可視化分析及其對稀相氣力輸送中壓降的影響。 Powder Tech。,179,170(2008)。 [ 鏈接 ]
Xiong,W.,Kalkühler,K。和Merzhirch,W。,流量調節器下游的速度和湍流的測量。 In:流體計量流體力學(Ed.Merzkirch,W。),Springer,Berlin,pp.61-78(2005)。 [ 鏈接 ]
- 上一篇:你知道稀相真空氣力輸送系統嘛?
- 下一篇:氣力輸送工程現場照片